PROFITER DE LA CSG
Construire et rendre une scène simple dans AYAM
Construire une scène consiste à modéliser des objets
volumiques et à les mettre en scène en utilisant un outil dédié, le modeleur. Rendre la scène, c'est restituer
une vison photo-réaliste de celle-ci par l'entremise d'un autre outil spécifique,
le moteur de rendu. Parfois, les modeleurs
intègrent leur propre moteur de rendu (Moonlight Atelier 3D, Equinox-3D,
Blender...), parfois, ils font appel à un moteur externe tel que PovRay,
BMRT, VirtualLight, Aqsis, Air.... C'est le cas du modeleur libre multi-plateforme AYAM qui fait appel par défaut au moteur,
multi-plateforme aussi, BMRT
Nous nous proposons de réaliser les tâches précitées: construire la scène
dans AYAM, en utilisant les fonctions
CSG, et la rendre dans BMRT. Un seul prérequis: la connaissance minimale
de l'interface de AYAM et du recours
à ses fonctions de base.
1 Deux ou trois choses à propos de la CSG:
Il ne s'agit pas de la Contribution Sociale Généralisée,
à laquelle tout contribuable est astreint, mais de combinaisons simples de
volumes de base, appélés Primitives,
afin de constituer un volume complexe qu'il eût été impossible de modéliser
autrement. On comprend bien qu'en additionnant des sphères, cubes, cones,
tores... c'est à dire des Primitives,
on constitue un objet de forme tarabiscotée; on comprend encore qu'en soustrayant
d'autres primitives au premier objet composé on obtiendra une forme davantage
compliquée: cette façon de faire s'appelle CSG,
c'est à dire Constructive Solid Geometry,
une des plus anciennes méthodes de modélisation 3D, qui s'appuie sur les
opérations booléennes. Il 'agit en fait
d'opérations simples, Union, Différence et
Intersection (et quelques dérivés: Merge, Inverse, Clipping) qui
doivent leur nom au mathématicien anglais George Boole
(1815-1864) qui mit au point en 1846 une algèbre logique, l'algèbre de Boole,
définissant des relations logiques de réunion, d'intersection et de complémentation.
Qu'on ne s'affole pas: les opérations seront effectuées par l'ordinateur,
l'utilisateur se contentant de signaler au programme quel genre d'opération
il souhaite voir réalisées entre deux primitives de son choix.
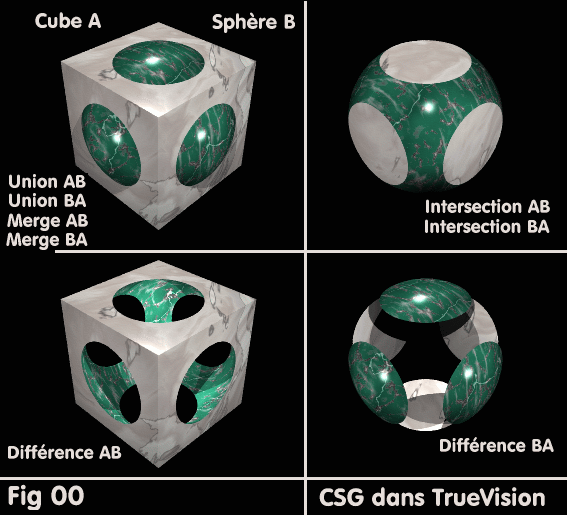
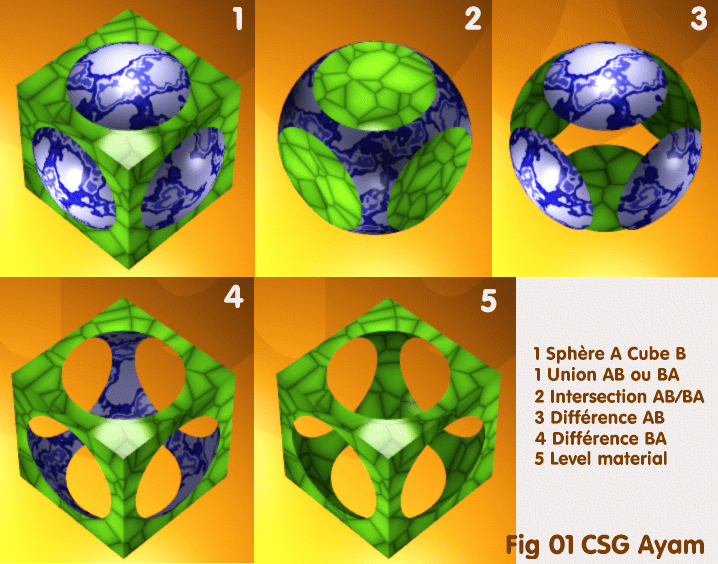
Exemple: soit un cube A et une sphère B, les deux primitives, imbriqués comme
sur la Fig00: "CSG dans TrueVision".
Les opérations Union AB et Union BA seront visuellement et logiquement
identiques: les deux primitives existent toujours avec leurs caractéristiques
propres mais seront considérées lors de manipulations ultérieures comme un
seul et même objet.
Les opérations Merge AB et Merge BA seront visuellement identiques à Union, mais les objets perdent leurs caractéristiques
propres au droit de leur volume commun. Les deux objets ont fusionné en un
seul.
Les opérations Intersections AB et Intersection BA seront visuellement et logiquement
identiques, puisque Intersection ne conserve
que la partie commune aux deux objets, et supprime le reste. La partie commune
de A et B est évidemment identique à la partie commune de B et de A.
Les opérations Différence AB et Différence BA donnent des résulats différents.
Dans le premier cas, il s'agit de soustraire B à A, donc d'enlever la sphère
au cube, alors que dans le second, il s'agit de soustraire A à B, c'est à
dire d'enlever le cube à la sphère.
2 Mise en oeuvre dans AYAM
Ayam dispose des trois opérations élémentaires Union, Différence
et Intersection, dont le mode opératoire
est conforme à ce qui a été dit précédemment. Toutefois, alors que la simplicité
voudrait que l'on indique au programme que l'on veut effectuer une Intersection(par esxemple) entre les primitives A et B, il faut, dans AYAM, créer d'abord les objets à traiter,
puis créer un objet résultant d'une CSG,
c'est à dire un objet Level, ensuite
préciser quelle est la nature de l'opération par LevelAttr
> Intersection, et enfin, par un tirer-déposer (Drag'Drop)
à partir de l'arbre de construction, introduire dans Level les objets A et B, dans l'ordre. Cette
démarche est identique à celle que l'on rencontre dans KPovmodeler, Moray
et, à un degré moindre, Cinema 4D.
En résumé:
-Créer une Sphère A et un Cube B
-Les positionner relativement l'un à l'autre
-Créer un Level
-Renseigner LevelAttr
-Placer Sphère dans Level
-Placer Cube dans Level
Et... rien ne semble avoir changé.
En effet, tout comme dans KPovmodeler, le résulat de l'opération n'est visible
que dans un rendu, ce qui est une faiblesse de ces deux programmes. Moray
dipose d'une fonction Evaluate qui permet de voir l'opération en mode filaire.
A noter également: si le matériau (shader) des objets leur a été affecté avant
la CSG, les surfaces visbles des objets
après l'opération conservent leurs attributs propres. Si aucun matériau n'a
été attribué aux objets participants, il suffira d'en attribuer un à l'objet
Level, et toutes les surfaces visibles
auront l'aspect de ce matériau. Voir Fig 01: "CSG
Ayam".
3 Modéliser les objets de base
Nous nous proposons de modéliser un dé à jouer. Celui-ci,
si l'on y regarde de près, n'est pas un simple cube. En effet, il faut qu'il
puisse rouler sur un tapis et qu'il puisse également interrompre sa course
dans une position stable. Pour ces raisons, les arêtes et les sommets du dé
sont arrondis, et il présente 6 faces planes sur lesquelles il peut s'arrêter.
En l'examinant encore plus attentivement, on s'aperçoit que le dé est constitué
d'une sphère à laquelle on a ôté 2 fois 3 calottes orthogonales.
Ainsi défini comme le résultat d'une soustraction
de volumes à un autre volume, le dé est parfait pour être obtenu par CSG, la soustraction (différence) étant une opération booléenne.
Il y a deux façons de procéder pour le cas présent: soit construire une sphère,
l'entourer de 6 cubes correctement disposés et sosutraire les cubes à la sphère.
C'est une méthode trop complexe.
L'autre façon consiste à imbriquer une sphère dans un cube et à réaliser l'intersection des deux volumes, afin de ne
conserver que leur partie commune. Bien évidemment, on va recourir aux Primitives existantes Box et Sphere
pour imbriquer la sphère et le cube.
Avant et après opération booléenne, les deux Primitives
se présentent dans AYAM comme sur laFig 1: "Les éléments de base".

Afin d'obtenir les mêmes résultats que ceux présentés
dans ce didacticiel, il convient de construire des volumes de dimensions identiques
à celles du didacticiel. Ainsi, cube (Box)
et sphère (Sphere) resteront positionnés
à 0,0,0. L'echelle du cube ( Fenêtre Main >Objects:
Box; Properties > Transformations >Scale) sera portée à
2 suivant X, Y et Z. L' échelle de la sphère sera portée à 1.4. Attention: Ne pas oublier de valider les changements
par Apply pour chaque modification, sur
chaque volume.
4 Opérer dans le vif
L'arbre de construction (Fenêtre Main> Objects)
contient pour le moment les objets Root, Box et Sphere.
Comme il a déjà été dit, les opérations booléennes passent par la création
d'un objet spécial, l'objet Level, auquel
on affectera l'attribut Intersection.
Marche à suivre:
-Fenêtre Main >Create > Level > Level
puis:
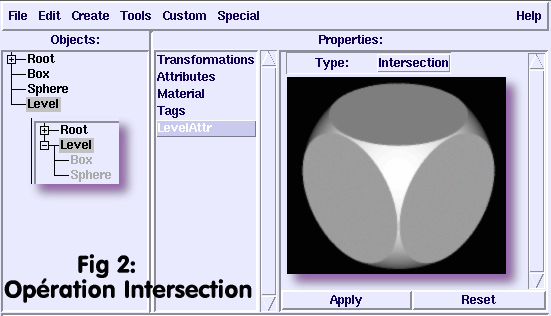
-Main >Objects Level; Properties LevelAttr >Type:
Intersection.
A noter que l'on peut directement créer un objet Level
Intersection en suivant le même cheminement.
Ceci étant fait, deposer à partir de l'arbre de construction, Box puis Sphere
dans Level, par drag'drop. L'arbre de
construction avant et après manipulation doit ressembler à Fig 2:" Opération Intersection".
5 Faire le(s) Point(s)
Les points sur les faces d'un dé sont des demi-sphères
imprimées en creux. On comprend aisément ici aussi que l'on obtiendra ce résultat
par un soustraction de matière. Toutefois, il s'agit de faire preuve d'un
minimum de ruse si l'on veut s'épargner un fastidieux labeur. En effet, un
dé compte un total de vingt et un points. Va-t'on effectuer vingt et une soustractions
de une sphère (Difference)? Ou bien va-t'on
pouvoir effectuer une seule soustraction de vingt et une sphères? Evidemment,
la facilité nous entraîne vers la deuxième solution, qui est effectivement
possible en procédant comme suit:
-Créer une sphère, modifier son échelle pour 0.2 sur X, Y et Z.
-Disposer la sphère sur la face voulue du dé.
-Puis par recopie (Main> Edit> Copy / Paste
ou Ctrl-c Ctrl-v) créer les autres sphères
et les mettre en place.
-Créer un objet Level Union.
-Placer toutes les sphères-points dans cet objet
Level
-Afin de clarifier la lecture de l'arbre de construction, renommer Level Intersection en Faces_Cube (Main>
Objects Level; Poperties Attributes> Objectname: Face_Cube)
-Renommer Level Union en Les_Points, et chaque sphère-point en Point1, Point3_1
etc,.
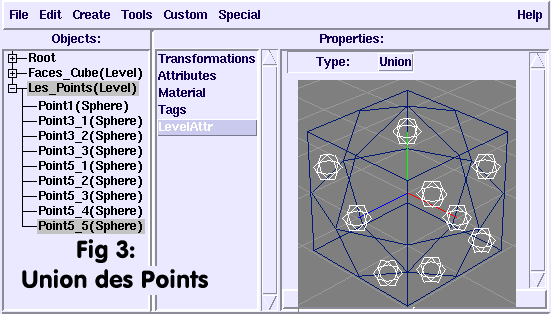
L'arbre de construction et la vue filaire de travail devrait ressembler à
la Fig 3: "Union des points", (qui est
capturée pour les points sur 3 faces seulement)
6 Percer les faces et finaliser le dé
Pour l'heure, les vingt et une sphères sont toujours
des sphères "en relief" sur les faces du dé. Il faut donc les "enfoncer" dans
les faces comme si elles étaient des poinçons, et les retirer ensuite pour
que ne demeurent visibles que leurs empreintes. Une opération booléenneDifference permet l'obtention de cet effet. Comme
précédemment, opérer ainsi:
- Creer un objet Level Difference
-Le renommer De_Final.
-Placer dans cet objet De_Final, l'objet
Face_Cube puis l'objet Les_Pointsen respectant cet ordre de hierarchisation.
C'est aux faces que l'on soustrait les points et non l'inverse.
-Créer un materiau pour le cube Mat_Cube
(Surface: shader plastic; RiAttributes: color 255,0,0).
-Créer un matéraux pour les points Mat_Points
(Surface: shader plastic; RiAttributes: color 255,255,240)
-Affecter ces matériaux par drag'drop aux objets concernés, c'est dire en
déplaçant l'objet et en le déposant sur le matériau qu'on veut lui affecter.
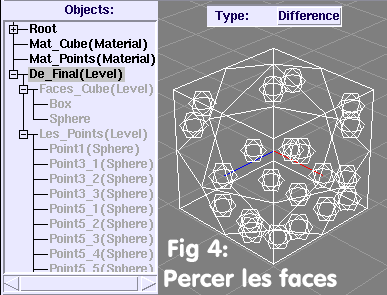
L'arbre de construction et la vue filaire de travail devraient ressembler
à la Fig 4: "Percer les Faces".
7 Vérifier le résultat
Tout le travail fastidieux est enfin terminé. Il est donc temps de se donner
quelque satisfaction en effectuant un rendu de la scène minimaliste ainsi
réalisée. Simultanément, l'opération de rendu permettra de se rendre compte
des effets de la
CSG qui, rappelons-le,
ne sont visibles ni en filaire ni en rendu rapide (
Quick
Render). Le résultat étant plus significatif en vue perspective
qu'en vue orthogonale, se rendre dans la vue
Persp
> View> Render.
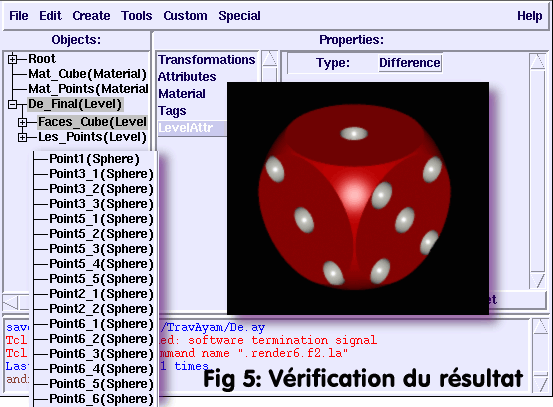
BMRT se lance et, normalement, le résultat
devrait ressembler à celui de la
Fig 5: "Vérification
du résultat".
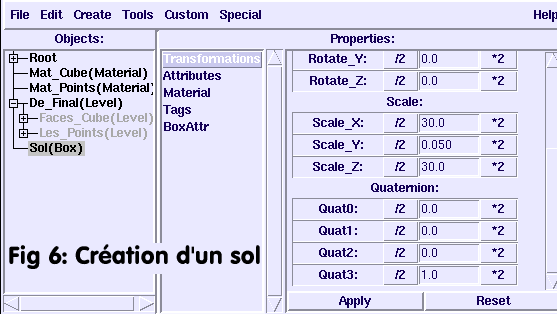
8 Création d'un sol.
A partir de maintenant, tout devient simple et gratifiant parce que la moindre
modification aura un grand effet. Par exemple: l'ajout d'un support au dé,
qui pour l'instant se trouve en apesanteur dans le noir. Ceci consiste en
la création d'un sol, composé d'un cube (
Box)
dimensionné tel que:
Scale X: 30 Y:0.05 Z:30.
Evidemment, ce sol devra être positionné de sorte que le dé repose sur lui
(on peut déplacer le dé plutôt que le sol, au grè de chacun).
Voir Fig 6: "Création d'un sol".
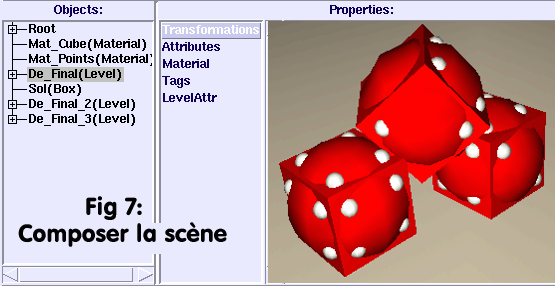
9 Composer la scène.
Un dé sur un sol, c'est un peu rudimentaire. On peut
donc multiplier les dés par Main> Edit> Copy
/ Paste. Les dés copiés occupent par défaut la même place que
le dé source. Pour les déplacer, il suffit de les sélectionner dans l'arbre
de construction, qui contient maintenant deux objets supplémentaires portant
le même nom que l'original De_Final (Level).
Evidemment, il conviendra de renommer les nouveaux venus d'une manière explicite,
tel que De_Final_2 et De_Final_3, afin de pouvoir sélectionner
sans erreur l'objet voulu. Tout cela est une évidence, qu'il est quand même
bon de rappeler.
Chacun disposera les dés à sa convenance. Une vérification en Quick Render sera suffisante pour contrôler
les modifications. La Fig 7: "Composer la scène"
propose une disposition des dés les uns par rapport aux autres.
A mon avis, une accumulation de dés identiques ne serait
pas d'un grand intérêt, sauf à les empiler d'une manière tout à fait originale
et esthétique. Au contraire, un dé d'une autre couleur pourrait rompre la
monotonie de l'uniformité, en apportant une note singulière, ou en captant
le regard pour le diriger vers un endroit de l'image que l'on voudrait mettre
en évidence. Quelle qu'en soit la raison, ajouter un autre dé par la même
méthode du copier-coller. Ce nouvel objet ne différe en rien des autres,
puisque la copie est conforme à l'original, tant en forme qu'en attributs
de matériau.
Si l'on veut que ce dernier dé différe, il va falloir créer deux nouveaux
matériaux que l'on affectera à ses faces et à ses points. De même, il convient
d'en créer un pour le sol: pourquoi pas un vert, style tapis de jeu (Surface: shader orennayar; RiAttributes: 0,146,0)?
Ne pas oublier non plus d'éclairer la scène avec trois spots à 120°, dont
un seul projettra une ombre. Les caratéristiques essentielles des spots (Intensity, ConeAngle, ConeDAngle) sont fonction
de l'ambiance de scène désirée, et de la position des spots par rapport aux
objets.
Effectuer enfin un rendu de la vue perspective, afin d'obtenir quelque chose
d'approchant à Fig 8: "Un Dé de plus?".

10 Fignolons, fignolons: c'est le fond qui manque le moins.
La scène commence a avoir un peu d'allure. Mais que
font ces quatre dés empilés, perdus sur un tapis? Ils paraissent déposés
là artificiellement. Ont-ils été jétés à la main? A l'aide d'un gobelet?
Directement sur un tapis de carte à jouer ou dans l'aire close d'un plateau?
Selon ce que la scène doit transmettre (le plus souvent: rien du tout. Elle
cherche juste à susciter une émotion), il convient d'y rajouter des éléments.
Par exemple , un plateau à bordure de bois, posé sur l'aluminium bouchonné
d'une table de bistrot. C'est juste une suggestion, facile à mettre en oeuvre.
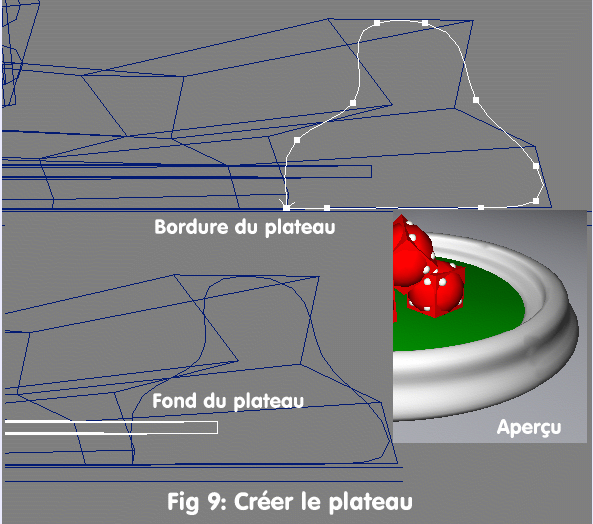
Un plateau est constitué d'un Fond (
Cylinder Scale
X:12, Y:0.1, Z:12) et d'une Bordure réalisée par révolution (
Revolve) d'une
ICurve,
le tout étant réalisé dans la vue
Front.
Pour manipuler simultanément les objets
Fond
et
Bordure, il est impératif de les hierarchiser
en un seul objet:
Plateau. Pour ce faire
créer un
Level Primitive, le renommer
Plateau, et y déposer par drag'drop les
objets
Fond et
Bordure.
Le matériau tissu vert existant déjà, l'attribuer au
Fond du plateau, et en créer un nouveau (
Surface: shader wood2) et l'attribuer à l'objet
Bordure du plateau.
Voir Fig 9: "Créer le plateau".
11 En a-t'on fini?
Un rendu de la scène élaborée montre que celle-ci se suffirait telle quelle.
Mais en réalité, pour celui qui s'adonne à l'imagerie de synthèse, une scène
est toujours susceptible de modifications, si ce n'est pas d'améliorations.
Ainsi, il apparaît que l'on pourrait lui adjoindre le gobelet permettant
de secouer les dés avant de les lancer, et de le poser un peu au hasard,
afin que l'ensemble dégage une impression d'un subit abandon du jeu, comme
si l'on craignait un sort funeste issu des dés jetés....
A chacun de voir.
Le gobelet étant très facile à modéliser, il n'en sera rien dit sinon qu'il
est rendu réfléchissant par l'usage du shader shiny
et d'une texture d'environnement couleur argent. Voir Fig 10: "Scène finale".

Que dire de plus. Ce travail est simple et suffisamment
rapide à exécuter pour ne pas se sentir découragé en cours de route, comme
on peut l'être avec des travaux dont on ne voit pas la fin. De plus, il montre
la plupart des possibilités de AYAM associé
à BRMT, qui valent vraiment la peine
que l'on se penche sur eux. Alors: mettez-le en oeuvre...
Bonne synthèse à tous.