9.3 A fractal example: Van Koch snowflake

Using recursion, it’s very easy to generate in LOGO some special curves called fractals in mathematics.



Here are the first steps to create the Van Koch broken line:

Between two steps:

1. each segment is divided into three equal part.
2. an equilateral triangle is drawn on the middle segment.
3. finally, this middle segment is erased.

What is important: Let’s have a look at step 2, we can see that the broken lines contains four identical motifs corresponding to precedent step with a 3 lesser size. Here we have found the recursive structure of the fractal.



Let’s call L_n,ℓ the motif of size ℓ, corresponding to step n.

To draw this motif:

1. We draw L_{n−1,ℓ∕3}
2. We turn left 60 degrees
3. We draw L_{n−1,ℓ∕3}
4. We trun right 120 degrees
5. We draw L_{n−1,ℓ∕3}
6. We trun left 60 degrees
7. We draw L_{n−1,ℓ∕3}

With LOGO, it’s very easy to write:

                                                                                                  
                                                                                                  
 # :l motif size
 # :p step
 to line :l :p
 if :p=0 [fd :l] [
   line :l/3 :p-1 lt 60 line :l/3 :p-1 rt 120 line :l/3 :p-1 lt 60 line :l/3 :p-1
 ]
 end

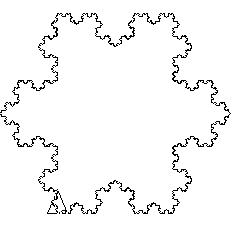
If we draw an equilateral triangle with three Van Koch lines, we obtain a beautiful Van Koch snowflake.

 # :l side length
 to snowflake :l :p
 repeat 3[line :l :p rt 120]
 end

Then run: snowflake 200 6