Transformations géométriques Par Xavier Michelon

Retour à OpenGL :

Revenons maintenant à OpenGL. Si vous vous rappelez le didacticiel précédent, je vous ai indiqué comment faire tourner le cube avec la fonction glRotatef(). Grâce au paragraphe précédent, vous allez pouvoir comprendre ce que font réellement la fonction glRotatef() et les autres fonctions de transformation que nous allons voir.

La bibliothèque OpenGL met à la disposition du programmeur trois matrices : une matrice de transformation-visualiation (celle qui nous intéresse aujourd'hui), une matrice de projection, et une matrice de texture. Ces trois matrices sont stockées dans des structures de données internes à la bibliothèque, et en général, l'utilisateur n'y accède directement. Afin de travailler sur ces matrices, OpenGL définit une matrice "active", c'est-à-dire la matrice sur laquelle vont être effectuer les transformations qui suivront. Pour choisir la matrice active, on utilise

glMatrixMode(GLenum mode)  

Le paramètre "mode" désigne la matrice que l'on souhaite activer. Il peut prendre comme valeur GL_MODELVIEW, GL_PROJECTION, et GL_TEXTURE. Pour effectuer des transformations sur les objets de la scène, il faut modifier la matrice de transformation-visualisation (GL_MODELVIEW). Nous reviendrons sur les deux autres matrices dans les prochains didacticiels. Par défaut, la matrice de modélisation-visualisation est la matrice active, ce qui explique pourquoi nous n'avons pas eu besoin d'utiliser glMatrixMode() la dernière fois.

Définir une transformation avec OpenGL consiste à placer la matrice correspondant à cette transformation dans la matrice de modélisation-visualisation. Bien qu'il soit possible de spécifier directement les 16 coefficients de la matrice active grâce à la fonction glLoadMatrix(), on procède en général autrement, en utilisant les fonctions glLoadIdentity(), glRotate(), glTranslate et glScale().

void glLoadIdentity();

cette fonction a pour effet de placer dans la matrice active la matrice dite d'identité, représentée sur la figure 6. Cette matrice correspond à une transformation nulle : les points ne sont pas déplacés. Pour vous en convaincre, multipliez une matrice d'identité par un vecteur P, vous verrez que le résultat du produit n'est autre que P. Quel en est l'intérêt ? Cette fonction permet de "remettre à zéro" la matrice de transformation.

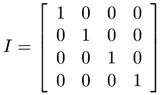Figure 6 : La matrice identité

void glTranslatef(float x,float y,float z);

Cette fonction (et sa variante glTranslated() dont les paramètres sont de type 'double') multiplie (à droite) la matrice active par une matrice de translation de vecteur (x,y,z).

void glRotatef(float theta,float x,float y,float z); 

Cette fonction multiplie la matrice active par une matrice de rotation d'angle thêta autour de l'axe passant par l'origine et porté par le vecteur (x,y,z).

void glScalef(float hx,float hy,float hz);

Cette fonction multiplie la matrice active par une matrice de d'homothétie dont les facteurs suivant les axes X, Yet Z sont respectivement hx, hy et hz.

Prenons un exemple concret : on souhaite placer dans la matrice de modélisation-visualisation une matrice correspondant à une translation de vecteur (0,1,0) suivie d'une rotation d'angle 45° autour de l'axe Z. En notant Mt la matrice de translation et Mr la matrice de rotation, on désire placer dans la matrice active le résultat du produit Mr.Mt (rappelez vous que l'ordre d'écriture des matrices est inversé par rapport à l'ordre d'application des transformations). La portion de code OpenGL pour accomplir cette tâche est la suivante :

glLoadIdentity();
glRotatef(45.0,0.0,0.0,1.0);
glTranslatef(0.0,1.0,0.0);

A priori, on ne sait pas ce qui se trouve dans la matrice, et donc avant d'effectuer la moindre opération, il convient de la réinitialiser en y plaçant la matrice identité avec un appel à glLoadIdentity(). on enchaîne ensuite les transformations à ajouter dans la matrice, puis on peut commencer la description de l'objet 3D. Lorsque vous spécifiez un point de l'espace, OpenGL lui applique la transformation contenue dans la matrice de modélisation-visualisation, et l'objet entier subit donc la transformation.