Transformations de visualisation et autres Par Xavier Michelon

Pour illustrer toutes les notions que nous avons étudié aujourd'hui, je vous propose un exemple un peu plus élaboré que les précédents : une ballade virtuelle dans un pièce contenant 4 objets, le tout en vue fil de fer (figure 2).

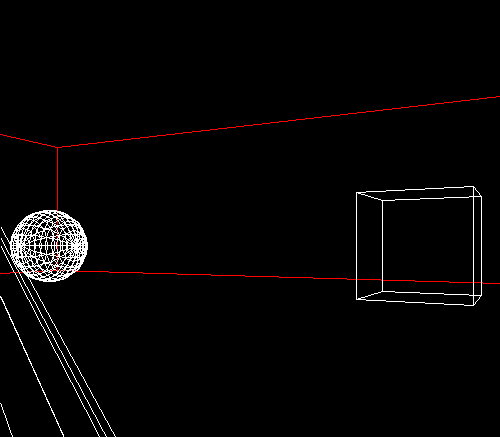Figure 1: le programme exemple

La scène est composée de 5 primitives : deux cubes (dont un qui représente les murs de la pièce), un cône, une sphère et un tore. Décrire chacun de ces objets point par point serait fastidieux, et nous allons donc faire appel à glut pour nous aider : en effet, l'API de Mark Kilgard contient des fonctions qui se chargent pour nous de décrire les primitives suivantes : sphère, cube, cone, tore, dodécaèdre, octaèdre, tétraèdre, icosaèdre et .... théière ( allez faire un tour sur http://web2.iadfw.net/sjbaker1/software/teapot.html si vous voulez savoir pourquoi la théière est considérée comme un primitive en infographie). Par exemple, glutWireSphere(x) permet de générer un sphère de rayon x  en vue fil de fer. Si vous souhaitez affichez une sphère pleine, utilisez glutSolidSphere(). La description des fonctions de génération de primitives est disponible dans la documentation glut dont l'adresse est citée dans les références.

La pièce est un cube de 20 unité de longueur auquel on a appliqué une homothétie de rapport 0.25 suivant l'axe des Y. Elle est centrée en l'origine. Les quatre autres objets sont placés dans le cube et sont "posés" sur le sol.

Gestion du point de vue et des déplacements :

On souhaite pouvoir déplacer l'observateur à l'intérieur de la scène. Pour cela, on s'impose les règles suivantes :

• L'observateur peut se déplacer n'importe où dans la pièce. En notant px et pz la position de l'observateur (par défaut, l'axe y est l'axe vertical), cela revient à dire que px et pz doivent être compris entre -10 et +10.
• L'observateur peut avancer en appuyant sur la touche 'z' et reculer avec  la touche 's'.
• L'observateur peut tourner sur lui même (en appuyant sur le bouton gauche de la souris puis en déplaçant celle-ci horizontalement).
• L'observateur regarde toujours l'horizon. il ne peut ni lever ni baisser la tête.

Pour repérer notre utilisateur dans la pièce, nous utiliserons trois variables : px, pz (position de l'observateur) et r (angle indiquant la direction dans laquelle l'utilisateur regarde (voir figure 3)).

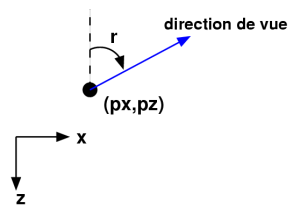Figure 3 : positionnement de l'utilisateur

Au lancement du programme, l'utilisateur est positionné à l'origine, et il regarde en direction de l'axe des z négatif, ce qui revient à dire que px=pz=r=0.Quand l'utilisateur avance de n unités dans la direction dans laquelle il regarde, il suffit pour calculer sa nouvelle position de décrémenter pz de n*cos(r) et d'incrémenter px de n*sin(r).

D'un point de vue implémentation, vous trouverez dans les fonctions de rappel souris et clavier (keyboard(), mousePress() et mouseMotion()) le code permettant la mise à jour des valeurs de px,pz et r. Vous noterez la présence d'une fonction testPosition() qui est appelée dès qu'on modifie la valeur de px ou pz. Elle s'occupe simplement de vérifier que l'utilisateur reste à l'intérieur de la pièce. La valeur de référence est de 9.8, afin d'éviter les problèmes de clipping qui peuvent se produire si vous venez vous coller contre le mur. Vous noterez également la présence de la fonction calcCosSinTable(). Nous utilisons dans nos calculs de position les opérateurs mathématiques sinus et cosinus dont les temps d’exécution sont relativement longs. Pour ne pas ralentir l'application, on précalcule les cosinus et sinus pour les valeurs allant de 0 à 359, et on les stocke dans deux tableaux. Bien sûr, ceci nous force à n’utiliser que des valeurs d’angle entières.

Dans la fonction display(), vous remarquerez l'utilisation de la pile de matrice : on spécifie tout d'abord les transformations de visualisation, puis on copie la matrice dans la pile. On décrit ensuite chaque objet de la scène (avec les transformations qui lui sont appliquées). Entre chaque description, on dépile la matrice afin que de récupérer la matrice contenant simplement les transformations de visualisation. Attention, après avoir récupéré la matrice par un glPopMatrix, il faut replacer un copie de la matrice dans la pile si vous souhaitez décrire encore plusieurs objets.

En ce qui concerne la projection, le programme donne la possibilité à l'utilisateur de modifier le champs de vision depuis le clavier avec les touches ‘b’ et ‘n’. La définition du mode de projection de passe dans la fonction changePerspective(), qui correspond au modèle présenté plus haut.