Le cube tournant en OpenGL Par Xavier Michelon

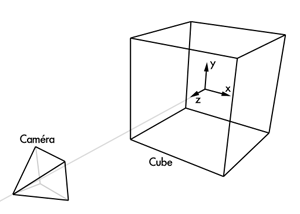
Figure 1 : La scène 3D

Si on fait le compte, notre cube comporte 6 faces et 8 sommets. La scène est encore assez simple (si on la compare aux dizaines de milliers de sommets que comportent généralement les scènes crées par les professionnels de l'infographie), et on pourrait tout à fait se contenter, comme nous l'avons fait dans le précedent didacticiel, de décrire linéairement chaque polygone. Nous allons cependant mettre en place une structure de données pour stocker notre scène. OpenGL fournit des fonctions permettant la mise en place de structures de stockage, mais nous allons voir qu'il est tout à fait possible de le faire soi-même.

Première chose, nous allons définir un type de données pour stocker chaque point : il s'agit d'une structure composée de 6 nombres de type flottant qui contient les coordonnées cartésiennes du point (x, y et z), ainsi que la couleur du sommet (r, g et b).

typedef struct
{
  float x;
  float y;
  float z;
  float r;
  float g;
  float b;
} point; 

Pour stocker tous les sommets de la scène, on définit un tableau de points, et on en profite pour le remplir avec les coordonnées des points de notre cube et leurs couleurs :

point p[8]={
    {-0.5,-0.5, 0.5,1.0,0.0,0.0},
    {-0.5, 0.5, 0.5,0.0,1.0,0.0},
    { 0.5, 0.5, 0.5,0.0,0.0,1.0},
    { 0.5,-0.5, 0.5,1.0,1.0,1.0},
    {-0.5,-0.5,-0.5,1.0,0.0,0.0},
    {-0.5, 0.5,-0.5,0.0,1.0,0.0},
    { 0.5, 0.5,-0.5,0.0,0.0,1.0},
    { 0.5,-0.5,-0.5,1.0,1.0,1.0}};

Reste maintenant à trouver une structure permettant de stocker les 6 faces de notre cube. Sachant qu'une face comporte exactement 4 sommets, nous pouvons utiliser un tableau à 2 dimensions contenant les indices (dans le tableau p que nous venons de créer) de chacun des points de la face :

int f[6][4]={
  {0,1,2,3},
  {3,2,6,7},
  {4,5,6,7},
  {0,1,5,4},
  {1,5,6,2},
  {0,4,7,3}};

Ce tableau peut à première vue paraître obscur, aussi voici de quoi éclairer votre lanterne : f[i][j] contient l'indice du j-ième sommet de la face numéro i. Ainsi, la face numéro 4 est définie par les sommet p[1], p[5], p[6] et p[2] (je vous rappelle qu'en C, les indices de tableaux commencent à 0, et non à 1).