Génération de terrain (1/2) Par Xavier Michelon

La pratique

Le code source de notre générateur de terrain reprend bon nombre de routines que nous avons déjà utilisées plusieurs fois (rotation, zoom, redimensionnement) et il utilise toutes les fonctionnalités que nous avons évoquées aujourd’hui. Il utilise deux listes d’affichage : une pour afficher le terrain et une pour afficher le repère XYZ. Le masquage des faces arrière est utilisé (vous avez la possibilité de le désactiver pour voir la différence), et on peut activer ou désactiver le masquage de l’arête transversale des patches.

La routine de lecture d’image JPEG à été légèrement modifiée de façon à permettre de charger une image en niveaux de gris de taille fixe (256x256). Vous avez la possibilité de passer en argument au programme l’image de votre choix. Elle doit simplement avoir un taille de 256x256 et être en niveaux de gris. Si vous ne passez aucune image en argument, le programme charge une image par défaut Toujours concernant la routine de chargement d’image, je tiens à signaler une petite erreur commise au cours des deux derniers didacticiels : dans les routines de chargement de fichier JPEG et TIFF, il n’est pas nécessaire de réorganiser les données lues, puisqu’elles sont déjà bien ordonnées. Il suffit d’étudier l’organisation en mémoire des deux structures pour se rendre compte qu’elles sont en fait identiques. Merci à Laurent Vuibert qui a été le premier à signaler cette bourde.

La création du terrain

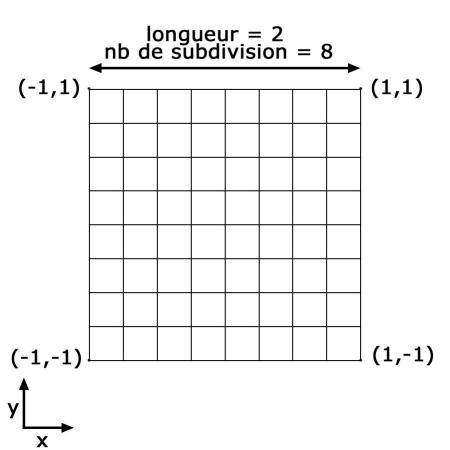
Le terrain est de dimension fixe : il s’agit d’un carré dans le plan XY dont les extrémités sont les point (-1,-1),(-1,1),(1,-1),(1,1). On souhaite pouvoir faire varier la densité de notre maillage avec les touches ‘+’ et ‘-’. Pour représenter la densité de notre maillage, on utilise un constante noté nbSubdiv qui représente le nombre de subdivisions sur chaque axe (voir figure 4). Si nbSudiv=4, le maillage est constitué de 4x4=16 patches. La fonction creeTerrain() prend en charge la définition de la liste d’affichage permettant de générer le terrain :

void creeTerrain()
{
  int i,j;
  float pas=2.0/nbSubdiv;
  float P1[3],P2[3],P3[3],P4[3];

  /* Liste pour l'objet terrain */
  if (glIsList(terrain))
    glDeleteLists(terrain,1);
  terrain=glGenLists(1);
  glNewList(terrain,GL_COMPILE);
  glColor3f(0.0,0.0,0.0);
  glLineWidth(1.0);
  for (i=0;i<nbSubdiv;i++)
    for (j=0;j<nbSubdiv;j++) {
      P1[0]=-1.0+i*pas; P1[1]=-1.0+j*pas ; P1[2]=elevation(i,j);
      P2[0]=-1.0+(i+1)*pas; P2[1]=-1.0+j*pas ; P2[2]=elevation(i+1,j);
      P3[0]=-1.0+(i+1)*pas; P3[1]=-1.0+(j+1)*pas ; P3[2]=elevation(i+1,j+1);
      P4[0]=-1.0+i*pas; P4[1]=-1.0+(j+1)*pas ; P4[2]=elevation(i,j+1);

      glBegin(GL_TRIANGLES);
      /* triangle 1 */
      glEdgeFlag(TRUE);
      glVertex3fv(P1);
      glVertex3fv(P2);
      if (!areteTransv)
        glEdgeFlag(FALSE);
      glVertex3fv(P3);

      /*triangle 2 */
      glVertex3fv(P1);
      if (!areteTransv)
        glEdgeFlag(TRUE);
      glVertex3fv(P3);
      glVertex3fv(P4);
      glEnd();
    }
  glEndList();
}

Figure 4: Subdivision du maillage

Le dessin du maillage se fait par une boucle imbriquée avec deux variables i et j. Le cœur de la boucle dessine le patch situé dans la i+1-ième ligne et la j+1-ième colonne. Le sommet supérieur gauche de ce patch se situe au point (-1+i*pas,-1+j*pas,Z) si on considère que ‘pas’ désigne la largeur d’un patch, c’est à dire 2/nbSubdiv. Les trois autres points du patch se calculent en incrémentant correctement i et j. La coordonnées en Z des sommets et calculée dans la fonction élévation() :

float elevation(int i,int j)
{
  int valeur=image[(int)((float)i/nbSubdiv*255)][(int)((float)j/nbSubdiv*255)];
  return ((float)valeur/128.0-1.0)*echelleVert;
}

elevation(i,j) renvoie la hauteur du sommet supérieur gauche du patch de la i+1-ième ligne et la j+1-ième colonne. La valeur retournée par élévation est comprise entre –echelleVert (si le pixel est noir) et +echelleVert (si le pixel est blanc). Vous pouvez faire varier l’échelle verticale echelleVert avec les touches ‘p’ et ‘o’.

Bien entendu, nous appliquons le découpage du patch en 2 triangles qui nous permettra d’éviter les problèmes d’éclairage. Vous avez la possibilité d’activer et de désactiver le masquage de l’arête transversale (en fait, il y en a 2, une par triangle) avec la touche ‘t’. Vous noterez également que l’argument passé à glBegin() n’est pour une fois pas GL_POLYGON, mais GL_TRIANGLES. En mode GL_TRIANGLES, les sommets décrits sont automatiquement groupés par trois pour créer des triangles. Ceci évite de devoir utiliser une seconde paire d’instructions glBegin()-glEnd() pour créer le second triangle constituant chaque patch.